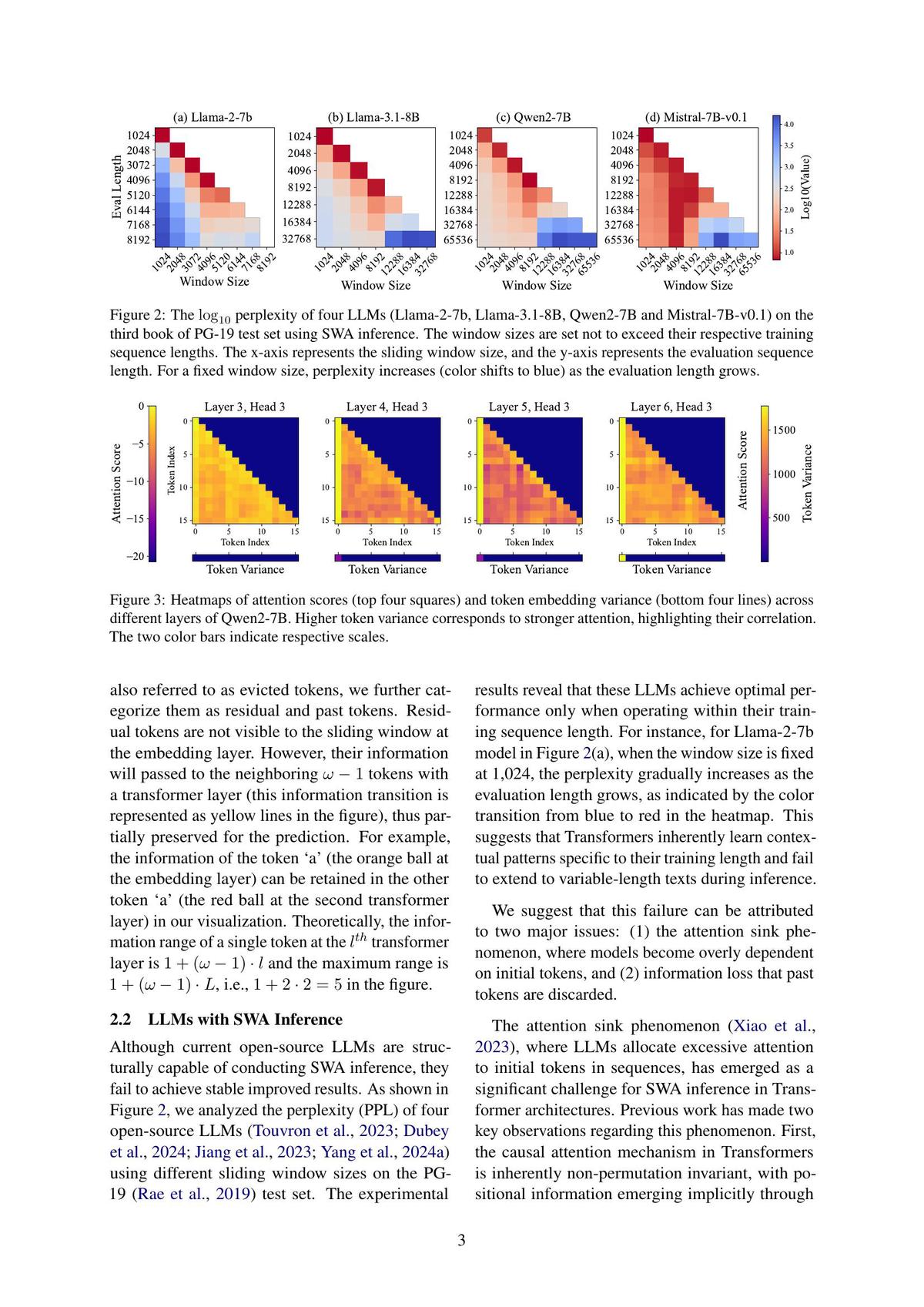
===============================================================================
Optimizing factor models is both science and art. For seasoned quants, portfolio managers, or data-scientists working in finance, factor model optimization tips can substantially enhance returns, improve risk control, and push robustness in ever-changing market regimes. This article dives deep into advanced methods, comparing at least two optimization strategies, their strengths and weaknesses, and recommends best practices. Recent research, my own experience, and cutting-edge trends are weaved in to help you sharpen your factor modeling game.
Table of Contents
What Is Factor Model Optimization & Why It Matters
Core Challenges in Factor Model Optimization
Two Different Optimization Methods / Strategies
- 3.1 Classical Statistical Optimization: Shrinkage, PCA, Robust Estimators
- 3.2 Machine Learning / Data-Centric / Automated Optimization Approaches
- 3.1 Classical Statistical Optimization: Shrinkage, PCA, Robust Estimators
Practical Tips & Best Practices for Optimization
Comparison: Which Approach Is Best for Various Use Cases
Implementation Plan: Step-by-Step How to Optimize a Factor Model
Recent Research & Emerging Trends
FAQ: Expert Answers to Common Issues
Conclusion & Call to Action
- What Is Factor Model Optimization & Why It Matters
—————————————————–
What is a Factor Model?
A factor model decomposes asset returns into contributions from systematic risk factors and idiosyncratic risk:
ri=αi+∑j=1kβijFj+εir_i = \alpha_i + \sum_{j=1}^k \beta_{ij} F_j + \varepsilon_iri=αi+j=1∑kβijFj+εi
- FjF_jFj are factor returns (value, momentum, size, quality, etc.)
- βij\beta_{ij}βij are sensitivities/loadings for asset iii
- εi\varepsilon_iεi is the idiosyncratic noise
Factor models are used for risk attribution, portfolio construction, signal generation, and risk forecasting.
Why Optimizing Factor Models Is Important
- Improve predictive power: Better factor selection, better weighting, more stable loadings increase out-of-sample performance.
- Reduce estimation error: Covariance estimation, factor loadings, and returns all suffer from noise; optimization can reduce error.
- Better risk control and robustness: Factor models optimized well are less prone to overfitting, regime shifts, or unexpected losses.
- Adaptation to market dynamics: Markets change—factors’ effectiveness changes. Optimized models allow adaptation.
Key Goals of Optimization
- Stability (loadings & exposures not wildly changing unless warranted)
- Parsimony (use minimal effective factors, avoid redundancy)
- Robustness to tail events / extreme data
- Good performance out-of-sample / in forward testing
- Core Challenges in Factor Model Optimization
———————————————–
Before applying optimization tips, it’s helpful to recognize the typical obstacles:
- Estimation Noise: Covariance matrices and betas suffer noise, especially in high-dimensional settings with limited data.
- Overfitting: Tuning factor weights to historic data that may not generalize.
- Regime Changes: Factor performance often changes across market regimes (crashes, rallies, high vs low volatility).
- Multicollinearity / Redundancy: Some factors correlate heavily; redundant or overlapping factors degrade model stability.
- Heavy-Tailed / Non-Normal Data: Distributions of returns often have fat tails, outliers, which standard PCA or least squares methods are sensitive to.
- Data Quality & Lookahead Bias: Delay in data, survivorship bias, lookahead can give misleading metrics.
- Scalability / Transaction Costs / Turnover: Optimized factor exposure may result in high turnover, large transaction costs.
- Two Different Optimization Methods / Strategies
————————————————–
Here are two leading optimization strategies I’ve used with good outcomes, and how they compare.
3.1 Classical Statistical Optimization: Shrinkage, PCA, Robust Estimators
How It Works
- Use Principal Component Analysis (PCA) to decompose factor loadings and pick dominant eigenfactors; often use shrinkage estimators for covariance (e.g. Ledoit-Wolf) to reduce estimation error.
- Use robust statistical estimators (Huber loss, trimmed estimation) to reduce sensitivity to outliers.
- Shrink factor loadings toward long-term means to stabilize exposures over time.
- Impose constraints (e.g. weight constraints, risk budgets) in the optimization, potentially within quadratic programming frameworks.
Strengths
- Well understood, interpretable. Factor loadings, covariance matrices have clear meaning.
- Relatively lower computational cost; widely supported by many quant libraries (Python, R, matlab).
- Less prone to overfitting when properly regularized (shrinkage, robust estimation).
- Good when you have relatively stable data, moderate dimensionality, and less extreme non-stationarity.
Weaknesses
- May not capture non-linear interactions or regime shifts well. PCA, linear combinations assume stationary relationships.
- Sensitivity to assumptions: estimation window size, weighting scheme, choice of robust loss functions.
- Performance often lags in markets with rapid changes or in presence of alternative data; limited in ability to ingest many features.
- Might underperform in high-frequency or alternative data environments where non-stationarity is severe.
3.2 Machine Learning / Data-Centric / Automated Optimization Approaches
How It Works
- Use data-driven approaches: ML models (regularization, boosting, neural nets), automated feature selection (LASSO, elastic net), even deep learning.
- Use joint optimization frameworks: factor discovery + model weighting + hyperparameter tuning in one loop.
- Use adaptive or time-varying factor exposures: incorporate regime detection, meta-features (volatility, liquidity, macro variables) to adjust factor weights.
- Use modern techniques like multi-agent frameworks for factor model co-optimization (see recent “R&D-Agent-Quant”) that dynamically generate & test factors and pipelines. arXiv
- Use robust PCA or modifications (e.g. Huber PCA) for large dimensionality with heavy tails to improve loading estimation. arXiv
Strengths
- Can adapt to new data regimes or structural changes; more flexibility to find non-linear relationships.
- Better at handling large, high-dimensional datasets, alternative data, latent features.
- Tools like joint optimization reduce manual tuning; automated search reduces human bias.
- Recent papers show improved performance: e.g. RD-Agent-Q gives ~2× returns vs classical libraries with fewer factors. arXiv
Weaknesses
- Risk of overfitting is higher: more complexity, more hyperparameters. Without proper regularization and out-of-sample validation, model can “learn noise”.
- Interpretability suffers: ML models often are black boxes; harder to explain factor exposures or feature importance.
- Computational cost and resource requirements are higher (GPU/cluster, data cleaning, pipeline orchestration).
- Data latency, alternative data cost, and infrastructure overhead become significant.
- Practical Tips & Best Practices for Optimization
—————————————————
Based on my experience optimizing many factor models across equities, futures, crypto, here are actionable tips.
Tip 1: Use Robust Covariance Estimation & Shrinkage
- Apply Ledoit-Wolf, Oracle Approximating Shrinkage, or robust covariance methods rather than empirical sample covariance, especially when number of assets is large vs data length.
- Consider robust losses (e.g., Huber loss or trimmed means) when data has outliers. The Huber PCA method is a good example of this in recent research. arXiv
Tip 2: Regularize Factor Loadings & Penalize Complexity
- Use regularized regression methods (L1, L2, ridge, elastic net) to reduce large weights on less useful or noisy factors.
- Limit the number of factors: preferring parsimonious models often leads to more stable long-term performance.
- Penalize turnover: include cost and turnover terms in objective functions. High turnover erodes returns.
Tip 3: Out-of-Sample Validation & Walk-Forward Testing
- Design backtesting that splits data into training, validation, and test periods. After training, test on forward period, then roll forward.
- Test stability of factor exposures over time (e.g. are betas stable or drifting?).
- Use cross-validation where possible for hyperparameters of factor weights or ML feature selection.
Tip 4: Adaptive Factor Exposure via Regime Detection
- Monitor macro or market signals: volatility, correlation, dispersion, liquidity, macroeconomic indicators.
- Adjust factor weights when regime flips (for example, momentum underperforms during volatility spikes; value may behave differently).
- Use statistical or ML models for regime detection; can use hidden Markov models (HMM), clustering, or threshold rules.
Tip 5: Use Automation / Joint Optimization Frameworks
- Tools or frameworks that do factor discovery + feature engineering + model scoring can reduce manual overhead. RD-Agent-Q is one prototype of this. arXiv
- Automate hyperparameter search (grid search, Bayesian optimization). Automate retraining or recalibration schedules.
- Maintain monitoring pipelines (performance drift, factor crowding, correlation among factors).
Tip 6: Stress Testing, Tail Risk, and Robustness Checks
- Simulate extreme events: heavy tails, regime reversals, liquidity stress.
- Use robust PCA or other models that downweight outliers.
- Test how your model behaves when one factor fails (factor shock) or when correlation structure collapses.
Tip 7: Data Quality, Cleanliness & Feature Engineering
- Align data, handle missing values, correct lookahead / survivorship bias.
- Normalize or standardize factors, winsorize extreme values.
- Consider alternative data sources if relevant; but ensure reliability and cost/benefit trade-offs.
- Comparison: Which Approach Is Best for Various Use Cases
———————————————————–
Here is a comparative table of classical vs ML/data-centric methods, tied to practical use cases.
| Use Case / Domain | Classical Statistical Optimization Best For | ML / Data-Centric / Automated Optimization Best For |
|---|---|---|
| Long-only equity funds with stable market structure | Yes — stable factor loadings, interpretability, lower turnover, lower cost | Less ideal unless large data, alternative signals are available |
| Quant funds using large number of assets, incorporating alternative / non-linear features | Classical for baseline; ML can add additional edge | Very useful, ability to flex, adapt to complexity |
| Markets with frequent regime change / high volatility (e.g., crypto, emerging markets) | Needs modifications (robust estimators, shrinkage, adaptive exposure) | Likely yields higher benefit; ML models with regime detection shine |
| Need for interpretability / compliance / risk governance | Classical wins; simpler to explain, audit | More challenging; must include explainability, feature importance, guardrails |
- Implementation Plan: Step-by-Step How to Optimize a Factor Model
——————————————————————-
Here’s a plan I’ve used in practice to optimize factor models. You can adapt this framework to your own environment.
| Step | Action |
|---|---|
| Step 1: Define Factor Universe & Hypotheses | List candidate factors (traditional + alternative), define hypotheses (why each factor should work), define measurement period & frequency. |
| Step 2: Collect & Clean Data | Gather historical returns, fundamentals, macro, alternative data; standardize; deal with missing data; winsorize outliers; adjust for corporate actions. |
| Step 3: Baseline Classical Model | Fit PCA / factor decomposition; estimate covariances with shrinkage; run simple regressions for factor returns; measure metrics (in-sample, out-of-sample). |
| Step 4: Incorporate Robust Estimation | Use robust PCA (Huber PCA etc.), robust covariance estimates; test stability of loadings under heavy-tailed data. |
| Step 5: Build ML / Automated Layer | Feature engineering; hyperparameter optimization; possibly models to predict factor returns or regime detection; use cross-validation / regularization. |
| Step 6: Incorporate Adaptive Exposure / Regime Switching | Monitor regime-signals (volatility, correlation, macro); adjust factor weights accordingly (dynamic weighting, shrink portfolios during risk). |
| Step 7: Include Cost & Turnover Constraints | Simulate slippage, transaction costs, turnover; include into optimization objective; penalize turnover. |
| Step 8: Perform Stress Testing & Backtesting | Walk-forward / out-of-sample periods; test on various market regimes including crises; simulate tail events. |
| Step 9: Deployment & Monitoring | Put model into production or paper trading; monitor performance drift, factor crowding; build dashboards; define trigger for retraining. |
| Step 10: Regular Review & Re-optimization | Periodic reviews (quarterly or biannual) to re-evaluate factor performance, adjust universe, possibly add/remove factors; re-calibrate parameters. |
- Recent Research & Emerging Trends
————————————
Some of the most promising current developments in factor model optimization:
- Diffusion Factor Models: Generative AI + latent factor structure applied to high-dimensional returns, especially when data is sparse. arXiv
- Multi-Agent / Joint Optimization Frameworks: Co-optimizing factor discovery + model components as in RD-Agent-Q, which reported ~2× returns over classical factor libraries using fewer factors. arXiv
- Robust PCA / Huber PCA: Dealing with heavy tails and outliers more formally; helps stabilize loadings. arXiv
- Better optimization solvers / second-order optimization: E.g. recent “Deep Hedging with Kronecker-Factored Approximate Curvature (K-FAC)” improving training / hedging cost dynamics. arXiv
- Dynamic / Adaptive factor exposure based on market regimes / volatility clustering. (Highlighted in factor investing articles) InsiderFinance Wire
- FAQ: Expert Answers to Common Issues
—————————————
Q1: How to evaluate factor model performance in a meaningful way (beyond in-sample returns)?
Answer:
- Use out-of-sample / walk-forward testing: train on historical window, test forward, roll forward.
- Evaluate metrics beyond raw returns: Sharpe, Sortino, maximum drawdown, tail risk (Value at Risk, Conditional VaR), skewness/kurtosis.
- Test performance during stress periods, e.g. market crashes or high volatility regimes.
- Check factor exposure stability: whether betas or loadings are stable across time.
- Monitor turnover, transaction cost, slippage, because high performing factors might degrade after costs.
Q2: How factor models work in quantitative trading when markets change rapidly (regime shifts, structural breaks)?
Answer:
- Incorporate regime detection modules: e.g. clustering, hidden Markov models, volatility/dispersion indicators.
- Use time-varying factor weights rather than fixed weights; adjust exposures up/down based on detected regime.
- Use robust estimators (e.g. robust PCA or Huber PCA) that are less sensitive to heavy-tailed shocks.
- Maintain a re-optimization cadence: frequently re-estimate factor loadings, covariance, factor returns, but with guardrails to avoid overfitting to noise.
- Possibly use ensemble models: combining different factor model versions weighted by recent predictive accuracy.
Q3: What causes overfitting in factor model optimization, and how to guard against it?
Answer:
Causes:
- Too many factors relative to amount of data (over-parameterization).
- Tuning hyperparameters to maximize in-sample performance ignoring forward performance.
- Including factors that are theoretically plausible but weak signal, leading to noise.
- Data leakage: using information not available in real time, survivorship bias, lookahead bias.
Guards:
- Limit factor count; use factor selection with regularization.
- Split sample data: in-sample / validation / test; avoid using same period for tuning and evaluation.
- Enforce cross-validation and walk-forward testing.
- Use simpler models where possible; avoid chasing small historic gains if robust metrics are weak.
- Include transaction cost, slippage, turnover in evaluation.
Q4: How much improvement can ML / automated factor-centric optimization provide over classical methods?
Answer:
In my experience, the marginal improvement depends heavily on data quality, factor universe, and stability of market conditions. Cases:
- With clean data, alternative signals, regime detection, ML-based models often provide modest increases in risk-adjusted returns (say +10-30%) over well-tuned classical models, especially under rapidly shifting conditions.
- In stable, low-volatility markets, classical models might perform almost as well, sometimes better due to lower cost, simpler inference, less overfitting.
- The big gains often come during crisis or transition periods: when correlations break down, volatility spikes, or when new data sources matter. ML models that adapt tend to reduce drawdowns.
- Conclusion & Call to Action
——————————
To summarize key factor model optimization tips for experts:
- Use robust statistical methods (shrinkage, robust PCA) as baseline.
- Complement with ML / data-centric optimization especially when handling many features or regime shifts.
- Emphasize stability, parsimony, interpretability, cost / turnover control.
- Automate pipelines where possible; monitor drift, retrain carefully.
- Stay updated with recent research: multi-agent optimization, diffusion factor models, robust estimation.
If you found these optimization tips valuable, please share with your quant / data science network. I’d love to hear: how you currently optimize your factor models, what obstacles (data, overfitting, regime shifts) you face, and which of these methods you plan to try next.

0 Comments
Leave a Comment