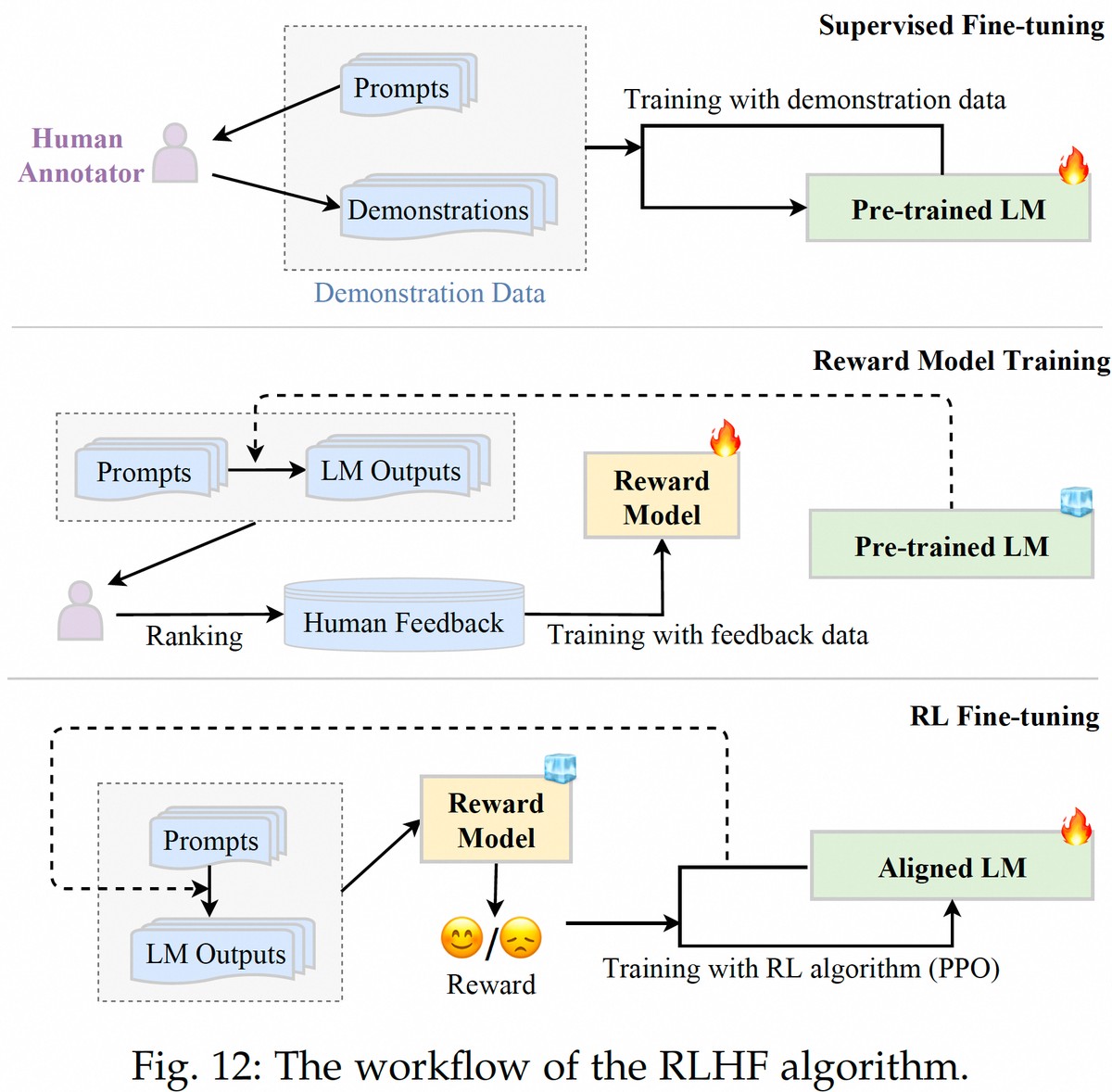
====================================================
Correlation is one of the most fundamental concepts in quantitative finance, risk management, and data-driven investment strategies. For anyone asking how to calculate correlation in quantitative models, the answer goes beyond a simple formula. Correlation is a vital tool to understand relationships between assets, improve portfolio diversification, and build predictive models in trading and research.
In this comprehensive guide, we will explore different methods to calculate correlation, compare their strengths and weaknesses, provide practical insights, and explain how professionals leverage correlation in real-world quantitative strategies.
Understanding Correlation in Quantitative Models
What Is Correlation?
Correlation measures the strength and direction of the relationship between two variables. In finance, it is often used to analyze how two assets move relative to each other. The correlation coefficient (commonly represented by ρ or r) ranges from -1 to +1:
- +1: Perfect positive correlation – assets move in the same direction.
- 0: No correlation – movements are unrelated.
- -1: Perfect negative correlation – assets move in opposite directions.
Why Is Correlation Crucial?
Quantitative researchers, traders, and portfolio managers rely on correlation for:
- Risk Management: Reducing exposure to highly correlated assets.
- Portfolio Optimization: Maximizing diversification benefits.
- Model Accuracy: Building robust predictive models with minimized redundancy.
This explains why is correlation important in quantitative analysis—it directly impacts decision-making across asset selection, trading strategies, and hedging.
Correlation coefficients visually illustrate relationships between two sets of data in quantitative finance.
Methods to Calculate Correlation
1. Pearson Correlation Coefficient
The Pearson method is the most widely used technique in quantitative models. It measures the linear relationship between two variables.
Formula:
r=∑(Xi−Xˉ)(Yi−Yˉ)∑(Xi−Xˉ)2∑(Yi−Yˉ)2r = \frac{\sum (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum (X_i - \bar{X})^2 \sum (Y_i - \bar{Y})^2}}r=∑(Xi−Xˉ)2∑(Yi−Yˉ)2∑(Xi−Xˉ)(Yi−Yˉ)
Advantages:
- Easy to compute.
- Works well when variables are linearly related.
- Suitable for large datasets.
Disadvantages:
- Sensitive to outliers.
- Only measures linear correlation, missing nonlinear patterns.
2. Spearman’s Rank Correlation
The Spearman method evaluates monotonic relationships by ranking data values before computing correlation.
Formula:
ρ=1−6∑di2n(n2−1)\rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)}ρ=1−n(n2−1)6∑di2
where did_idi = difference between ranks.
Advantages:
- Captures non-linear monotonic relationships.
- Less sensitive to outliers than Pearson.
Disadvantages:
- Computationally heavier for large datasets.
- May overlook fine-grained relationships.
3. Kendall’s Tau Correlation
Kendall’s Tau is another rank-based method that counts concordant and discordant pairs.
Advantages:
- More robust in small samples.
- Useful when dealing with ordinal data.
Disadvantages:
- Less commonly used in finance compared to Pearson and Spearman.
- Lower statistical power with large datasets.
4. Rolling and Dynamic Correlation
Quantitative finance often requires analyzing time-varying correlations. Rolling correlation applies a moving window over time series data.
Advantages:
- Tracks changing relationships across market cycles.
- Critical for portfolio risk monitoring.
Disadvantages:
- Window size selection heavily influences results.
- Can produce noisy signals.
Rolling correlation helps track dynamic relationships between assets over time.
Comparing Correlation Calculation Methods
| Method | Captures Linear? | Captures Nonlinear? | Robust to Outliers | Common Use in Finance |
|---|---|---|---|---|
| Pearson | ✅ Yes | ❌ No | ❌ Weak | Portfolio construction, regression models |
| Spearman | ✅ Yes (monotonic) | ✅ Yes | ✅ Moderate | Factor analysis, asset ranking |
| Kendall’s Tau | ✅ Yes (rank-based) | ✅ Yes | ✅ Strong | Small datasets, qualitative analysis |
| Rolling Correlation | ✅ Yes (time-based) | ❌ Limited | ❌ Variable | Dynamic risk monitoring |
Practical Applications in Quantitative Models
Portfolio Diversification
Correlation helps identify assets that move differently, reducing risk. For instance, equities and government bonds often show negative correlation during crises.
Risk Management
Hedge funds and institutional traders use correlation matrices to monitor exposures. Understanding why do quantitative traders use correlation matrices explains their role in systemic risk prevention.
Strategy Design
In algorithmic trading, correlation informs pair trading, market-neutral strategies, and factor models.
Case Study: Correlation in Portfolio Construction
During the 2008 financial crisis, many portfolios failed due to hidden correlations across supposedly diverse assets. By applying rolling correlation analysis, investors could have identified rising correlations and reduced exposure.
This demonstrates how does correlation affect quantitative trading by shaping both profitability and resilience.
Correlation matrices are essential tools for quantitative portfolio management.
Best Practices for Correlation in Quantitative Models
- Use Multiple Methods: Rely on Pearson for linear patterns, but validate with Spearman for robustness.
- Apply Rolling Windows: Detect shifts in relationships over time.
- Beware of Spurious Correlation: Always test statistical significance.
- Combine with Volatility Analysis: High correlation under stress often coincides with rising volatility.
- Leverage Technology: Modern platforms integrate real-time correlation analysis into dashboards.
Personal Insights from Practice
In my professional experience, relying solely on Pearson correlation often led to misleading conclusions. For example, in analyzing tech stocks, Pearson suggested strong positive correlation, but Spearman revealed non-linear divergences during earnings announcements. Using a hybrid approach—Pearson for long-term structure and Spearman for event-driven adjustments—provided more accurate signals.
Emerging Trends in Correlation Modeling
- Machine Learning Approaches: Using neural networks to capture complex, non-linear relationships.
- Copula Models: Better suited for modeling tail dependencies.
- High-Frequency Correlation Analysis: Used in intraday trading systems.
- Cross-Asset Correlation: Expanding models to include equities, bonds, FX, and crypto.
FAQ: How to Calculate Correlation in Quantitative Models?
1. What is the most reliable way to calculate correlation in finance?
The Pearson correlation is most common, but for robustness, professionals often combine it with Spearman or Kendall’s Tau, especially when datasets contain outliers or non-linear patterns.
2. How do rolling correlations improve risk management?
Rolling correlations track changing relationships over time, helping traders identify when diversification benefits weaken, particularly during market crises.
3. Can correlation be misleading in quantitative models?
Yes. Spurious correlation occurs when variables appear related but are not causally connected. Always check statistical significance and validate results with multiple methods.
Conclusion
Understanding how to calculate correlation in quantitative models is fundamental for researchers, traders, and risk managers. From Pearson’s simplicity to Spearman’s robustness and rolling correlation’s adaptability, each method has distinct advantages and limitations.
The best practice is to combine multiple techniques, integrate correlation matrices into trading platforms, and continuously monitor dynamic relationships. In an era of high-frequency trading and complex portfolios, mastering correlation analysis is not just useful—it is essential.
👉 Do you use Pearson, Spearman, or dynamic models in your work? Share your experiences in the comments and spread this article with colleagues exploring quantitative strategies.
Correlation analysis remains a cornerstone of quantitative finance and risk management.

0 Comments
Leave a Comment