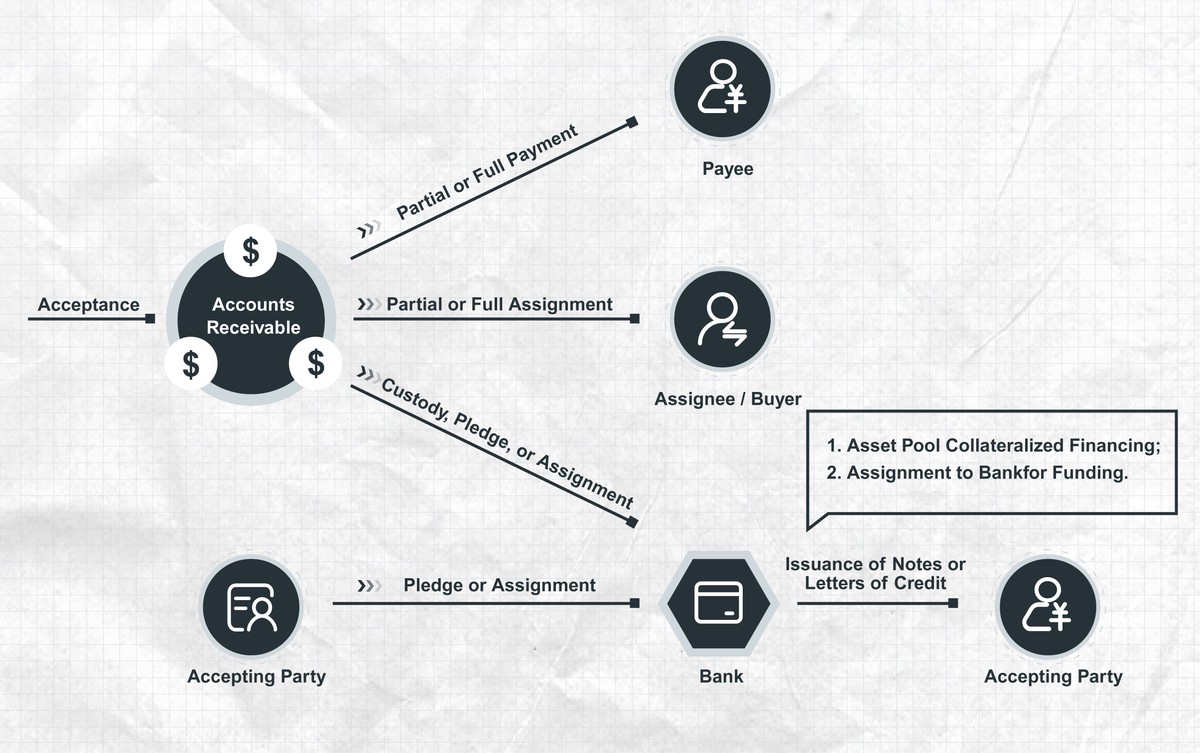
==========================================================
The information ratio (IR) is one of the most important performance metrics in quantitative trading. It helps traders and investors measure the efficiency of active returns generated relative to a benchmark, adjusted for risk. In this article, we will provide a step-by-step explanation of how to calculate the information ratio in quantitative trading, compare it with other performance measures, explore real-world applications, and review strategies for improving IR.
By the end, you will have a complete framework to not only calculate but also interpret and apply IR effectively in your trading or investment process.
What is the Information Ratio?
The information ratio measures the excess return of a portfolio over a benchmark, divided by the volatility of that excess return. It essentially tells us how much skill or value-added return a trader or portfolio manager generates per unit of risk.
Formula for Information Ratio
IR=Rp−Rbσ(Rp−Rb)IR = \frac{R_p - R_b}{\sigma_{(R_p - R_b)}}IR=σ(Rp−Rb)Rp−Rb
Where:
- RpR_pRp = portfolio return
- RbR_bRb = benchmark return
- σ(Rp−Rb)\sigma_{(R_p - R_b)}σ(Rp−Rb) = standard deviation of excess returns (tracking error)
A higher information ratio means the strategy is delivering consistent outperformance against the benchmark.
Step-by-Step Guide: How to Calculate Information Ratio in Quantitative Trading
Step 1: Define the Benchmark
Choose a relevant benchmark index that reflects the market or sector you are competing against. For example:
- Crypto traders may use BTC or ETH returns.
- Equity traders often use the S&P 500.
- Hedge funds may benchmark against custom factor models.
Step 2: Calculate Excess Returns
Subtract the benchmark return from the portfolio return:
Excess Return=Rp−RbExcess\ Return = R_p - R_bExcess Return=Rp−Rb
Example: If your portfolio earned 12% and the benchmark earned 8%, the excess return is 4%.
Step 3: Measure Tracking Error
Tracking error is the standard deviation of the excess returns over time. It quantifies how volatile the portfolio’s active returns are compared to the benchmark.
Tracking Error=σ(Rp−Rb)Tracking\ Error = \sigma_{(R_p - R_b)}Tracking Error=σ(Rp−Rb)
Example: If the standard deviation of excess returns is 2%, the tracking error is 2%.
Step 4: Compute the Information Ratio
Divide the average excess return by the tracking error:
IR=4%2%=2.0IR = \frac{4\%}{2\%} = 2.0IR=2%4%=2.0
This result indicates that the portfolio delivers two units of return for every one unit of active risk—an excellent result.
Real-World Example in Quantitative Trading
Consider a quantitative trading strategy that invests in a basket of growth stocks, benchmarked against the NASDAQ index.
- Portfolio annual return: 15%
- NASDAQ annual return: 10%
- Standard deviation of monthly excess returns: 3%
Excess Return=15%−10%=5%Excess\ Return = 15\% - 10\% = 5\% Excess Return=15%−10%=5%
IR=5%3%≈1.67IR = \frac{5\%}{3\%} \approx 1.67IR=3%5%≈1.67
This suggests the strategy generates reliable outperformance. Typically, an IR above 0.5 is considered acceptable, while IR above 1.0 is excellent.
Methods for Calculating and Applying Information Ratio
Method 1: Excel/Spreadsheet Calculation
Traders can use simple formulas in Excel or Google Sheets to calculate IR using portfolio and benchmark returns.
Advantages:
- Easy to set up
- Transparent calculations
- Suitable for beginner traders
Disadvantages:
- Manual data handling
- Prone to human error
Method 2: Python Quantitative Libraries
Libraries like Pandas, NumPy, and PyPortfolioOpt allow automated IR calculation and integration into algorithmic strategies.
Advantages:
- Scalable for large datasets
- Automatable for live trading systems
- Reduces manual errors
Disadvantages:
- Requires coding skills
- May need robust data pipelines
Comparison: Information Ratio vs. Sharpe Ratio
Many traders confuse IR with the Sharpe ratio. The key difference lies in the benchmark:
- Sharpe Ratio: Measures excess returns relative to a risk-free rate (e.g., U.S. Treasury yields).
- Information Ratio: Measures excess returns relative to a benchmark portfolio or index.
This distinction means IR is more relevant in active portfolio management, where the goal is to beat a benchmark, not just outperform cash. For deeper insights, it helps to understand how information ratio differs from Sharpe ratio, especially for institutional performance evaluations.
Why Information Ratio Matters in Quantitative Trading
- Skill Measurement: It helps distinguish luck from consistent trading skill.
- Risk-Adjusted Evaluation: Accounts for both return and volatility of active performance.
- Portfolio Optimization: Guides rebalancing decisions and model improvements.
- Institutional Reporting: Fund managers often publish IR in quarterly performance reviews.
As professional investors emphasize, knowing why information ratio is important in investing is critical for long-term credibility and capital inflows.
Visual Representation
This chart shows how consistent outperformance against a benchmark translates into a higher information ratio.
Advanced Insights: Improving the Information Ratio
- Optimize Strategy Parameters
Reduce unnecessary volatility by tuning trade entry and exit signals.
- Diversify Across Assets
Lower tracking error by combining uncorrelated strategies.
- Risk Controls
Avoid large drawdowns by using stop-loss mechanisms and dynamic position sizing.
- Data-Driven Enhancements
Apply machine learning models to refine signals and reduce noise in excess returns.
Frequently Asked Questions (FAQ)
1. What is a “good” information ratio?
A good IR is generally above 0.5. An IR above 1.0 indicates excellent active management, while above 1.5 is world-class. However, interpretation depends on the asset class and trading horizon.
2. Can information ratio be negative?
Yes. A negative IR means the strategy consistently underperforms its benchmark. In such cases, traders must reassess their models or risk management approach.
3. How often should I calculate the information ratio?
For quantitative traders, calculating IR monthly or quarterly is common. High-frequency traders may monitor it daily to assess system stability. The key is consistency in the measurement period.
Conclusion: Mastering Information Ratio in Quantitative Trading
Understanding how to calculate information ratio in quantitative trading is essential for evaluating performance, managing risk, and refining strategies.
- It provides a clear benchmark-relative measure of skill.
- Excel and Python both offer practical ways to calculate IR.
- Comparing IR with Sharpe ratio highlights its role in active portfolio evaluation.
- Traders can boost IR by diversifying, optimizing, and reducing tracking error.
By consistently applying these principles, traders and investors can make smarter decisions, improve performance, and demonstrate credibility in the eyes of clients and institutions.
👉 Found this guide useful? Share it with fellow traders, leave a comment with your approach to calculating IR, and join the discussion on improving performance in quantitative trading!
Would you like me to create a step-by-step Excel template for calculating Information Ratio, so readers can apply the method directly?

0 Comments
Leave a Comment