How to Analyze Option Data Quantitatively

=========================================

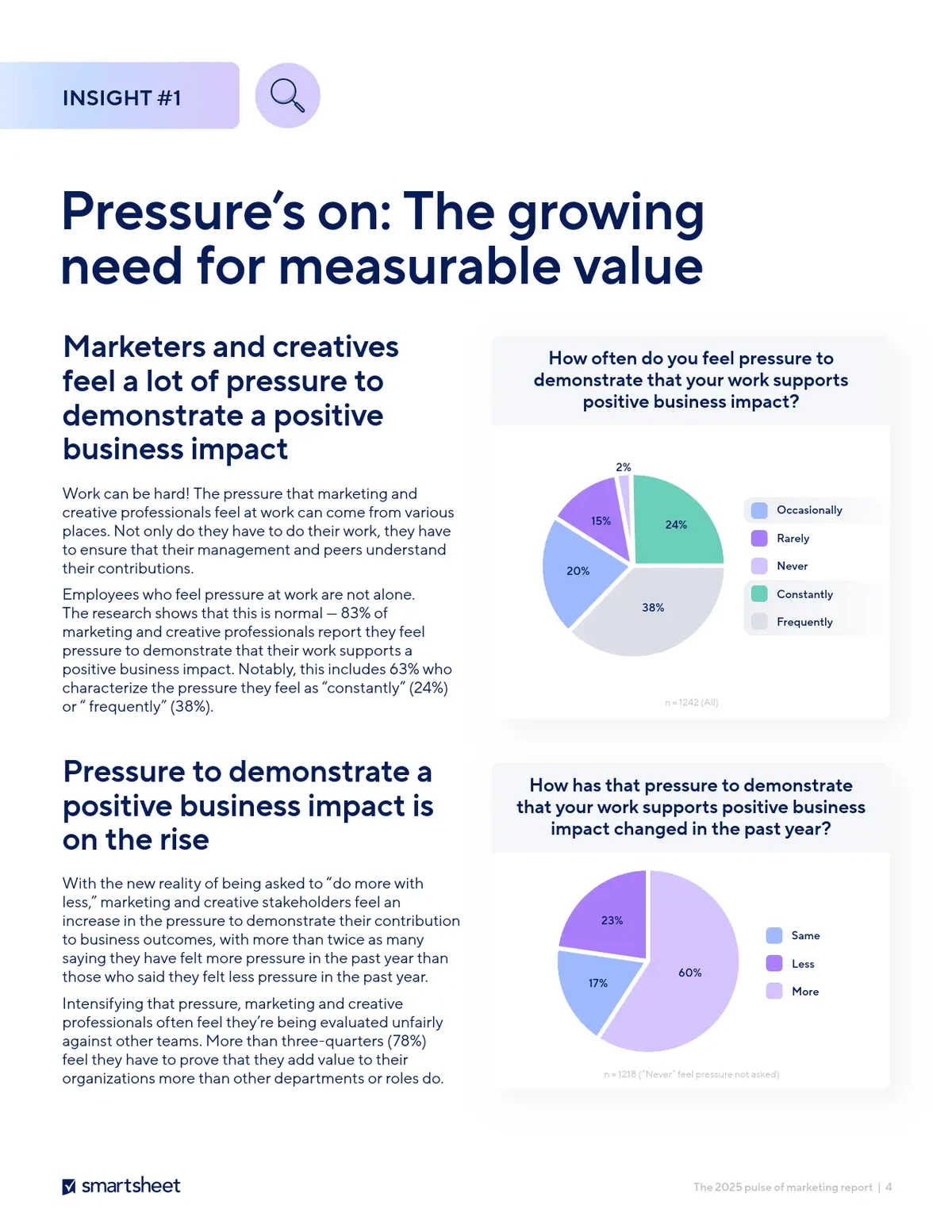
Options trading is a powerful strategy that allows traders to leverage their capital, hedge existing positions, or speculate on price movements. However, with the vast amount of market data available, analyzing options quantitatively has become a crucial skill for successful traders. This article explores how to analyze option data quantitatively, covering key techniques, methods, and tools to help you make informed decisions in options trading.

What Does Analyzing Option Data Quantitatively Involve?

Quantitative analysis in options trading involves applying mathematical models, statistical techniques, and computational tools to assess market conditions, determine potential price movements, and evaluate risk. By processing large amounts of historical and real-time data, traders can generate trading signals, backtest strategies, and optimize portfolios. Here are some core components of quantitative analysis in options:

Historical Price Analysis: Examining past price movements of options and underlying assets to identify patterns and predict future price behavior.
Implied Volatility (IV): Understanding how market expectations for volatility affect option prices.
Greeks: A set of metrics (Delta, Gamma, Theta, Vega, and Rho) used to measure an option’s sensitivity to various factors like price changes, time decay, and volatility.
Backtesting: Testing a trading strategy using historical data to evaluate its potential effectiveness.
Monte Carlo Simulations: Running simulations to model the potential outcomes of a trade or strategy under various conditions.

Key Methods to Analyze Option Data Quantitatively

1. Understanding and Using the Greeks

The Greeks are fundamental for analyzing option data because they help measure how sensitive an option’s price is to various factors. Let’s break down the key Greeks:

a. Delta

Delta measures the sensitivity of an option’s price to changes in the price of the underlying asset. It is particularly useful for understanding how much an option’s price will change for every $1 change in the price of the underlying asset. For example:

A Delta of 0.5 means that the option’s price will move $0.50 for every $1 movement in the underlying asset.

b. Gamma

Gamma is the rate of change of Delta as the price of the underlying asset changes. This helps traders understand how stable the Delta is, and can indicate potential changes in price movements, especially for options that are close to expiration.

c. Theta

Theta represents the time decay of an option’s price. As an option approaches expiration, its value typically decreases. Understanding Theta helps traders evaluate the time risk associated with their positions.

d. Vega

Vega measures an option’s sensitivity to changes in implied volatility. If implied volatility increases, the price of options tends to rise (especially for longer expiration dates). Traders often monitor Vega to assess potential changes in volatility.

e. Rho

Rho measures the sensitivity of an option’s price to changes in interest rates. While Rho tends to have a smaller impact on options compared to the other Greeks, it can still be important in environments where interest rates are changing rapidly.

By analyzing the Greeks, traders can gain insights into how various factors affect their options positions and adjust their strategies accordingly.

2. Implied vs. Historical Volatility

Volatility is one of the most critical factors in options pricing. There are two primary types of volatility to consider:

a. Implied Volatility (IV)

Implied Volatility represents the market’s expectation of future volatility and is directly factored into an option’s pricing. A high IV indicates that the market expects large price movements in the underlying asset, which will increase the option’s premium. Conversely, low IV suggests that the market expects smaller price fluctuations.

b. Historical Volatility (HV)

Historical Volatility refers to the past price fluctuations of the underlying asset. It is used to assess how volatile the asset has been in the past. While IV is forward-looking, HV is backward-looking and can be used to compare whether the market’s current expectations (IV) are high or low relative to past volatility.

To analyze options quantitatively, traders often compare IV and HV to identify opportunities. For example, if the IV is significantly higher than the HV, an options trader may view it as overpriced and look for strategies to capitalize on the mean-reversion of volatility.

Quantitative Tools for Analyzing Option Data

Several tools and software solutions can assist with the quantitative analysis of options data. These tools help with everything from calculating the Greeks to backtesting strategies and modeling complex scenarios.

1. Options Pricing Models

The most common model for pricing options is the Black-Scholes Model. This model is used to calculate the theoretical price of European call and put options based on several inputs, including the price of the underlying asset, the strike price, time to expiration, risk-free interest rate, and implied volatility.

While the Black-Scholes model is widely used, it’s important to note that it assumes constant volatility and interest rates, which may not hold in real markets. Other models, like the Binomial Option Pricing Model, allow for more flexibility and can account for changing conditions.

2. Backtesting Software

Backtesting software allows traders to test options strategies using historical data. By analyzing how a strategy would have performed in the past, traders can assess its effectiveness and fine-tune their approaches. Popular backtesting tools include:

QuantConnect: A platform that allows users to backtest trading strategies with historical data across multiple asset classes, including options.
MetaTrader ⁴⁄₅: A platform commonly used for forex and futures trading that also supports options backtesting.
ThinkOrSwim: A trading platform from TD Ameritrade that offers paper trading and backtesting capabilities for options.

Backtesting enables quantitative traders to refine strategies and make data-driven decisions.

3. Monte Carlo Simulations

Monte Carlo simulations are used to model the potential outcomes of a trading strategy under various conditions. This technique uses random sampling to simulate a range of possible price movements and calculate the expected value and risk of a strategy.

In options trading, Monte Carlo simulations can be particularly useful in modeling complex strategies involving multiple options or underlying assets. It provides a more dynamic and probabilistic view of risk compared to traditional analytical methods.

how to analyze option data quantitatively_2

Comparing Quantitative Methods for Option Data Analysis

1. Option Pricing Models (e.g., Black-Scholes vs. Binomial)

Both the Black-Scholes and Binomial models are widely used for pricing options, but they have key differences:

Black-Scholes Model: Ideal for European options, where exercise can only occur at expiration. It’s faster to compute but assumes constant volatility.
Binomial Model: More flexible, as it can model American options (which can be exercised at any time) and accommodates varying volatility over time. It’s computationally more intensive but more accurate in dynamic markets.

2. Implied Volatility vs. Historical Volatility

While both types of volatility are important, implied volatility is more forward-looking and directly impacts options pricing. However, implied volatility can be subjective, as it reflects market expectations, which may not always be accurate. Historical volatility, on the other hand, is based on actual data and can provide more objective insights into past market behavior. Quantitative traders often combine both to get a better sense of where the market is headed.

how to analyze option data quantitatively_1

FAQ: Analyzing Option Data Quantitatively

1. How can I use quantitative methods to predict future option prices?

Quantitative methods like option pricing models (Black-Scholes, Binomial) and volatility analysis can help predict option prices. These models take into account factors like implied volatility, time to expiration, and the price of the underlying asset. Monte Carlo simulations can also model different market scenarios to estimate future outcomes.

2. Why is it important to analyze the Greeks in options trading?

The Greeks provide essential insights into how an option’s price will react to various factors like changes in the price of the underlying asset, time decay, and volatility. By understanding the Greeks, traders can manage their risk and adjust their strategies to maximize profits or minimize losses.

3. What tools can help with quantitative options analysis?

There are several tools that can help with quantitative analysis of options, including backtesting platforms like QuantConnect, pricing models like Black-Scholes and Binomial, and simulation tools like Monte Carlo. These tools allow traders to model, test, and optimize their strategies effectively.

how to analyze option data quantitatively_0

Conclusion

Analyzing option data quantitatively is essential for traders who want to maximize returns and minimize risk. By leveraging tools like pricing models, the Greeks, implied volatility, and advanced techniques such as Monte Carlo simulations, traders can gain deeper insights into market dynamics and make more informed decisions. Whether you’re a beginner or an advanced trader, quantitative analysis provides a structured approach to trading options with greater confidence.

💬 How do you analyze option data in your trading strategies? Share your thoughts and experiences in the comments below, and feel free to share this article with fellow traders!