========================================
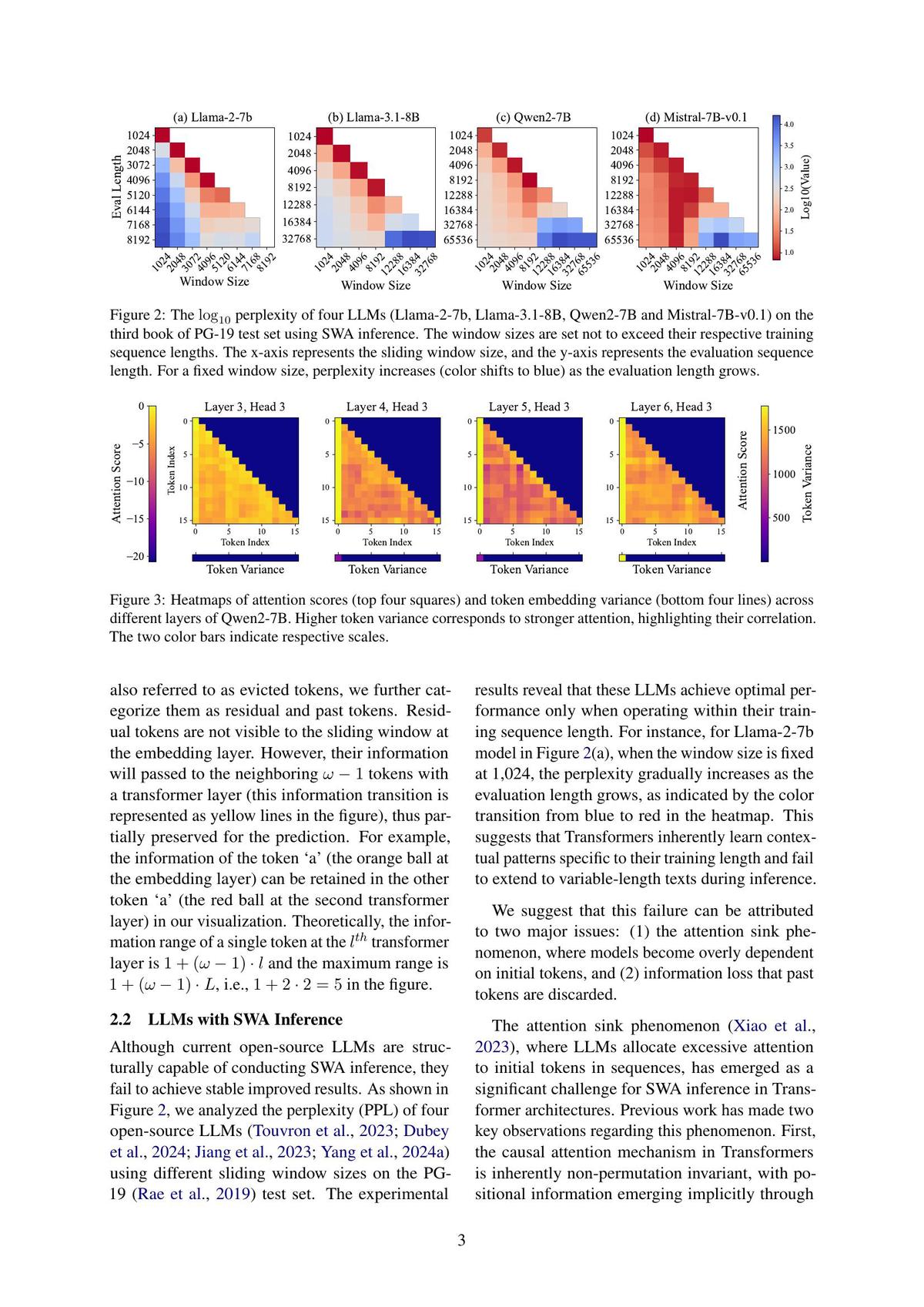
In the world of quantitative finance and investment strategies, factor models are essential tools for understanding and predicting asset returns. Evaluating the performance of a factor model is a crucial step in determining its effectiveness in identifying and explaining market trends. This article provides an in-depth guide on how to evaluate factor model performance, offering both theoretical insights and practical tips for applying factor models in real-world scenarios.
Table of Contents
Key Methods to Evaluate Factor Model Performance
- 2.1 R-squared and Adjusted R-squared
- 2.2 Alpha and Beta
- 2.3 Information Ratio
- 2.4 Tracking Error
- 2.5 Sharpe Ratio
- 2.1 R-squared and Adjusted R-squared
Advanced Factor Model Evaluation Techniques
- 4.1 Cross-validation
- 4.2 Bootstrapping
- 4.1 Cross-validation
Understanding Factor Models
Factor models are used in finance to explain the returns of assets based on various market factors. These factors could be anything from economic indicators (like interest rates and inflation) to market sentiment or technical factors (like price momentum and volatility). The primary purpose of factor models is to decompose asset returns into multiple components, which can help in portfolio management, risk management, and asset pricing.
There are two main types of factor models:
- Single-factor models, which focus on one specific factor (such as market returns).
- Multi-factor models, which involve multiple factors to explain asset returns more comprehensively.
Common examples of multi-factor models include the Fama-French Three-Factor Model and the Carhart Four-Factor Model, which incorporate factors like market risk, size, value, and momentum.
Key Methods to Evaluate Factor Model Performance
When evaluating the performance of a factor model, there are several key metrics and methods that investors and analysts use. These indicators help assess how well the model explains the asset returns and how reliable it is for future predictions.
2.1 R-squared and Adjusted R-squared
R-squared measures how well the factors in the model explain the variation in asset returns. An R-squared of 1 means the model perfectly explains the returns, while an R-squared of 0 indicates no explanatory power.
- High R-squared values suggest that the factor model is effective in capturing the underlying risk factors, but it doesn’t guarantee future performance.
- Adjusted R-squared takes into account the number of factors used and adjusts the R-squared value accordingly. This is useful for models with multiple factors, as it penalizes unnecessary complexity.
Example:
A factor model with an R-squared value of 0.85 means that 85% of the asset’s return variability is explained by the model’s factors, a strong indicator of model fit.
2.2 Alpha and Beta
- Alpha represents the excess return of an asset relative to its expected return based on the factor model. Positive alpha indicates that the asset has outperformed its predicted return, while negative alpha suggests underperformance.
- Beta measures the sensitivity of the asset’s return to the factor model. A high beta indicates that the asset is more volatile relative to the factors, while a low beta means it’s less volatile.
Example:
A factor model with a positive alpha of 2% implies that the asset outperformed the predicted return by 2%, indicating a strong predictive ability.
2.3 Information Ratio
The information ratio (IR) measures the risk-adjusted return of a factor model. It is calculated as the ratio of alpha to the tracking error, which measures how much the model’s predictions deviate from the actual returns.
- A higher information ratio signifies better performance, as it indicates that the model provides more return per unit of risk.
Example:
An information ratio of 0.5 means that for every unit of risk, the model generates 0.5 units of return above the benchmark.
2.4 Tracking Error
Tracking error measures how closely the factor model’s predicted returns track the actual returns of an asset or portfolio. A lower tracking error indicates that the model is more accurate in predicting the returns.
- High tracking error may suggest that the model is inconsistent or does not capture all the important factors driving returns.
Example:
A low tracking error of 2% indicates that the model’s predictions are very close to the actual returns, making it more reliable.
2.5 Sharpe Ratio
The Sharpe ratio is a widely used measure of risk-adjusted return. It is calculated as the average return of the model minus the risk-free rate, divided by the standard deviation of returns.
- Higher Sharpe ratios indicate better performance, as the model delivers more return per unit of risk.
Example:
A Sharpe ratio of 1.2 means that the factor model has generated a positive risk-adjusted return, which is desirable for investors seeking consistent performance.
Factor Model Backtesting
Backtesting is a critical method for evaluating factor model performance. It involves applying the factor model to historical data to assess how well it would have predicted past asset returns.
- Out-of-sample testing is particularly important to avoid overfitting, where the model fits past data well but fails to predict future returns accurately.
- Rolling window backtesting allows for continuous testing, ensuring that the model adapts to changing market conditions.
Advanced Factor Model Evaluation Techniques
While the basic evaluation methods above provide essential insights, more advanced techniques can further refine how factor models are assessed.
4.1 Cross-validation
Cross-validation involves splitting the data into multiple subsets to ensure that the model performs well on unseen data. It helps prevent overfitting and ensures the model’s robustness.
Example:
A factor model is trained on 80% of the data, and the remaining 20% is used for testing. The process is repeated with different data splits to validate the model’s performance.
4.2 Bootstrapping
Bootstrapping involves generating new datasets by resampling from the original dataset. It helps estimate the stability and reliability of the factor model under various scenarios.
Example:
Bootstrapping can be used to create multiple “artificial” datasets to test how the factor model performs under different market conditions.
Common Pitfalls in Evaluating Factor Models
While evaluating factor models, there are several common pitfalls to watch out for:
- Overfitting: This occurs when a model is too complex and fits the historical data too well, but fails to generalize to new data.
- Ignoring Market Changes: Factor models may fail to adapt to changing market conditions, making it important to continuously update and evaluate them.
- Over-reliance on Past Performance: Just because a model performed well in the past doesn’t mean it will perform well in the future. Always ensure models are validated using out-of-sample data.
Practical Examples of Factor Model Evaluation
Example 1: Multi-factor Equity Model Evaluation
A multi-factor model is built using factors like market returns, company size, and value to predict stock returns. The performance is evaluated using alpha and tracking error, finding that the model generates consistent excess returns with low tracking error, making it suitable for future use.
Example 2: Evaluating a Bond Market Model
A bond market factor model incorporates interest rates and credit spreads as factors. Backtesting over the past five years shows a high information ratio, suggesting the model is effective in generating risk-adjusted returns.
Frequently Asked Questions (FAQ)
1. How do I know if my factor model is overfitting?
Overfitting occurs when the model performs exceptionally well on historical data but poorly on out-of-sample data. To avoid this, use cross-validation and ensure the model is tested on unseen data to evaluate its generalization ability.
2. What is the best method to evaluate a factor model’s robustness?
Cross-validation and bootstrapping are effective methods to evaluate the robustness of a factor model. These techniques help ensure that the model performs well under various market conditions and is not overfitting to historical data.
3. How often should I update my factor model?
Factor models should be updated periodically to adapt to changing market conditions. Regularly backtest the model with out-of-sample data and incorporate new factors as necessary.
Conclusion
Evaluating factor model performance is crucial for investors looking to make informed decisions based on quantitative analysis. By using a combination of traditional and advanced evaluation methods, investors can assess the effectiveness of their factor models and ensure they remain robust in varying market conditions. Continuous testing, backtesting, and evaluation will help refine these models and improve investment strategies.
If you found this article helpful, please share it with others interested in factor model evaluation. Feel free to comment with your own experiences or questions

0 Comments
Leave a Comment